Leveraging Diversity and Sparsity in Blind Deconvolution
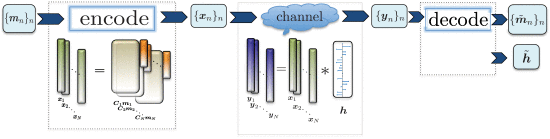
This paper considers recovering L-dimensional vectors w, and x 1 , x 2 , ⋯ , x N from their circular convolutions y_{n} = w * x_{n} , n = 1, 2, 3, ⋯ , N. The vector wis assumed to be S-sparse in a known basis that is spread out in the Fourier domain, and each input xn is a member of a known K-dimensional random subspace. We prove that whenever K+S log^{2} S \leq L/ log^{4} (LN), the problem can be solved effectively by using only the nuclear-norm minimization as the convex relaxation, as long as the inputs are sufficiently diverse and obey N \geq log^{2} (LN). By “diverse inputs,” we mean that the x_{n} ‘s belong to different, generic subspaces. To the best of our knowledge, this is the first theoretical result on blind deconvolution where the subspace to which w belongs is not fixed but needs to be determined. We discuss the result in the context of multipath channel estimation in wireless communications. Both the fading coefficients and the delays in the channel impulse response w are unknown. The encoder codes the K-dimensional message vectors randomly and then transmits coded messages x_{n} ‘s over a fixed channel one after the other. The decoder then discovers all of the messages and the channel response when the number of samples taken for each received message are roughly greater than (K + S log^{2} S) log^{4} (LN), and the number of messages is roughly at least log^{2} (LN).