Compressive Acquisition and Least-Squares Reconstruction of Correlated Signals

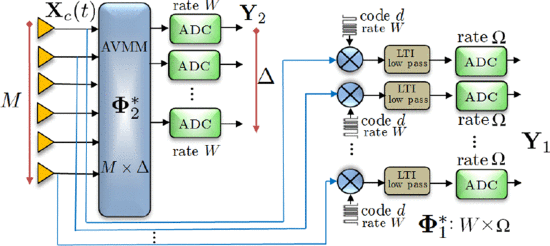
This letter presents a framework for the compressive acquisition of correlated signals. We propose an implementable sampling architecture for the acquisition of ensembles of correlated (lying in an a priori unknown subspace) signals at a sub-Nyquist rate. The sampling architecture acquires structured compressive samples of the signals after preprocessing them with easy-toimplement components. Quantitatively, we show that an ensemble of M correlated signals each of which is bandlimited to W/2 and can be decomposed as the linear combination of R underlying signals can be acquired at roughly RW (assuming without loss of generality M < W ) samples per second. In the case, when M \gg R, this results in significant reduction in the sampling rate compared to MW samples per second dictated by the Shannon-Nyquist sampling theorem. The signal reconstruction is achieved by solving only a least-squares program, which is in stark contrast to the prohibitively computationally expensive semidefinite programming techniques suggested in the earlier literature. We also provide rigorous analytical results to support our claims.