Channel Protection Using Random Modulation

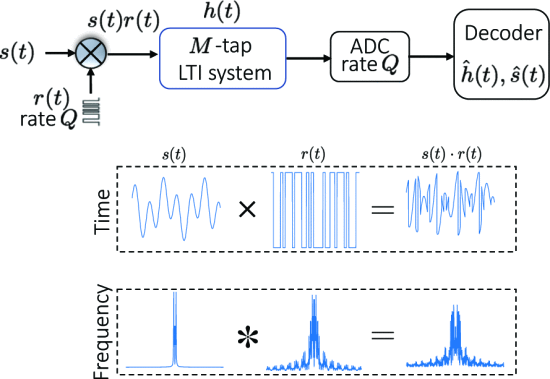
This paper shows that modulation protects a bandlimited signal against convolutive interference. A signal s(t), bandlimited to BHz, is modulated (pointwise multiplied) with a known random sign sequence r(t), alternating at a rate Q, and the resultant spread spectrum signal s(t) \odot r(t) is convolved against an M-tap channel impulse response h(t) to yield the observed signal y(t) = (s(t) \odot r(t)) \circledast h(t), where \odot and \circledast denote pointwise multiplication, and circular convolution, respectively.We show that both s(t), and h(t) can be provably recovered using a simple gradient descent scheme by alternating the binary waveform r(t) at a rate Q \geq B + M(to within log factors and a signal coherences) and sampling y(t) at a rate Q. We also present a comprehensive set of phase transitions to depict the trade-off between Q, M, and B for successful recovery. Moreover, we show stable recovery results under noise.